Nicholas B. BarkalovOne can not escape noticing that, as of the very end of the 20th century, the demographic analysis, i.e. the formal, statistical study of demographic processes, has changed quite profoundly from what the demographers were used to in the 1960s and early 1970s. The changes are noticeable with regard to its mathematical tools and techniques, methodological approaches, common practice of dealing with empirical data, if even in its very core conceptual issues. Two circumstances, in my view, are of the most principal importance therein. First. Whereas in the 1960s, a typical empirical (case) study of demographic processes was utilizing (pre-)tabulated (macro-)data on the composition (state) of a population under study and demographic events therewith, available chiefly from official statistical publications/releases (conventionally, the study was limiting its attention to respective age-specific rates), since the mid-1980s, virtually every published study was based on a collection of micro-data (i.e. individual records), obtained from available to researchers domains of a major retrospective survey, a micro-census (i.e.a large, up to 10-percent sample, national survey), and alike. The aforementioned gradual transition was essentially completed by the early 1990s. Thence, demographic indicators of interest for a given demographic-analysis task are no longer supplied by an external (published) source of tabulated data, but rather they are produced by the research demographer’s derivation from a micro-data set, which is typically a collection of individual demographic event-histories (sequences of demographic events, whose dates are recorded, occurred to a specific individual). There are basically two ways to proceed. The first one is a direct tabulation to obtain averages and distributions of an indicator in question with respect to specified demographic dimension(s). For instance, one obtains the distribution of the population of a specified age as of a specified calendar time (i.e. of an actual birth cohort) by the number of children ever born (current parity), marital or health status, etc. The second one begins with computing an occurrence-exposure ratio, for a given period of calendar time, specified by certain demographic dimensions (say, age, parity, marital status, length of open birth interval, etc.) The occurrence-exposure ratio thus produced becomes then the empirical base for implementing a chosen model that describes lifetime evolution of a hypothetical (synthetic) cohort. The model is implemented numerically by assigning the occurrence-exposure ratio’s value to its model counterpart (the so-called orientation equation). Obviously, the first way, i.e. the way of tabulations serves mostly for purposes of the actual-cohort (longitudinal) demographic analysis, while the second one supports the period (i.e. synthetic-cohort, or cross-sectional, transversal) demographic analysis. In fact, while the tabulated (macro-) data were limiting empirical implementation of the synthetic-cohort (period) analysis by supplying just few empirical quotients (in practice, the age-specific rates only), thus forcing demographers to deal with over-simplified models for lifetime evolution of a hypothetical (synthetic) cohort, which often produced evidently biased (and sometimes even inconsistent) estimates, hence discrediting the period demographic analysis in general, and contributing unfortunately to a false belief (particularly prevalent among older-generation demographers of Russia and France) that only actual-cohort estimates are reliable, the micro-data’s ability to produce a virtually unlimited host of the occurrence-exposure ratios has removed the mentioned constraint, making, actually for the first time in our science, the period demographic analysis a logically consistent and empirically sound tool for practical studies of investigating demographic processes. In my opinion, that constitutes the most important advantage which usage of the micro-data had brought to the field of demographic analysis. Fortunately, the recent decade was also marked with important theoretical contributions in the field of period demographic analysis (e.g. Ní Bhrolcháin 1992; Rallu and Toulemon 1993; Barkalov and Dorbritz 1996), chiefly with regard to fertility analysis, specifying and studying models for lifetime evolution of a hypothetical (synthetic) cohort, by far more refined than those conventional, solely-age based ones. The said advantage came at a price, though. While dealing with tabulated (macro-) data requires no data-processing job at all, the micro-data tabulations for purposes of the actual-cohort analysis can be performed relatively easily with widely available commercial software packages, like SPSS-PC, equipped with command interpreters, accessible to demographers with little or no programming experience. Not so for the synthetic-cohort based (period) demographic analysis that involves the occurrence-exposure ratios’ computation. It calls for a job of skilled professional programmers applying high-level programming languages (such as C, Pascal, Modula) with compilers into the object code (rather than command interpreters). The necessity to chose and apply, for measurement purposes, a formal model of a hypothetical (synthetic) cohort’s lifetime evolution, often a mathematically complex one, requires some higher skills from the demographer himself, too. To that, one adds the cost of micro-data per se, or more precisely, the cost of getting access to the data, which is not necessarily of proper financial, but perhaps, of operational, or political nature. My Russian-language note that supplements this paper (appearing in the present book as well) offers an overview of major collections of demographic micro-data currently available to Russian researchers and teachers of demography from international and national statistical data producing companies and projects, such as the Demographic and Health Surveys (DHS) in the less-developed countries, the Fertility and Family Surveys (FFS) in the UN European region, US and Russian national data sets, In particular, lower quality of the FFS data sets is noticed and commented on. I am also pointing out preferability (for statistical analysis, particularly for educational purposes) of a self-weighted, non-stratified data set (like those produced by the Russian micro-census of 1994, FFS collections for the Baltic and some East-European states) over a stratified one, each stratum of which appears with its own fixed weight. The procedures needed to obtain access to the data are discussed in the Russian-language supplementary note, as well. Second. During the 1990s, the contemporary tasks of demographic analysis had, in a way, shifted closer to the area of macro-economics, and undoubtedly became more politically charged, especially in less-developed countries, and crisis-ridden countries of ‘transitional economics’ (Russia among them). Although there had never been a sound rationale to presume that demographic processes (mortality and fertility primarily) could and should be studied chiefly as long-term, nay, secular, laminar trends, putting faster macro-economic and political changes on a background, both theoretical and empirical studies by Russian demographers had been mostly falling within that traditional presumption, particularly in a conceptual framework of the demographic transition. In the 1990s, however, the presumption mentioned became far less unchallengeable than it seemed before. Indeed, while the Russian Federation, accompanied by quite a few of its former Socialist neighbors had been dipped into a severe (if, possibly, well anticipated) economic and political crisis, the demographic crisis (the fertility level dropping to its all-time lows, mortality and morbidity rising, a formidable out-migration wave being sustained over decade) had arrived simultaneously, while apparently unexpectedly. Conclusively, it became quite a challenge to ignore the importance of shorter-term temporal variation in the demographic processes (mortality and fertility primarily), especially disregarding its commonly perceived link to the economic and political crisis. Meanwhile, in the broader Third World of less-developed countries, development projects and foreign-assisted programs had been extending onto the field of population qualitites away from their traditional narrower focus on proper macro-economic issues . Multi-lateral donors’ projects aiming to reduce HIV prevalence in Middle Africa serves as an example. In addition , national programs attempting to reduce the overall fertility levels, say, in China, India, South-East Asia, introduced earlier, had but acquired further attention and strategic interest. Therefore, it is not surprising that macro-demographic indicators, such as the life expectancy, theinfant mortality rate (IMR = q0), the under-five-age death rate ( 5q0, in the life-table notation), and the total fertility rate (TFR), i.e. measures originated within the realm of demographic analysis proper (rather than in a broader area of population studies) had been firmly placed in the list of strategically important national indicators watched closely by the national governments, international political organizations, and major trans-national corporations, on equal footing with conventional macro-economic indicators (like the GDP per capita, or the inflation rate), which had always been in the strategically important watch list. In fact, during the 1990s, one even notices an emergence of pseudo-scholarly works (e.g. the UN “Human Development” Reports) advocating to attach the prime importance to those macro-demographic indicators over the conventional, macro-economic ones. Undoubtedly, the strategic and political interest the macro-demographic indicators presently generate, lies entirely in the context of their short- and medium-run temporal evolution, i.e. developments comparable to macro-economic and political changes (major foreign-assisted programs in particular) the population in question is undergoing. In practice, that calls for a ‘faster’ demographic analysis, i.e. instant macro-demographic measurement and analytic evaluation, ideally, on an annual (year-by-year) basis, or involving averaging over no longer time periods than needed to establish statistically reliable estimates (normally, it’s either 3 or 5 calendar years). In this regard, it would not be reasonable, of course, to rely on the good old (indeed, in use since the 19th century) actual-cohort-based (longitudinal) methodology to supply required time series of the macro-demographic indicators. Rather, the celebrated methodology had been designed to represent numerically (in a simple and reliable way) those slow, generation-by-generation, not much faster, changes in the macro-demographic measures of demographic processes. In fertility analysis, in particular, the actual-cohort TFR appears as little more than a long-term average over the annual period TFR values (Ní Bhrolcháin 1992:610), hardly a good substitution for the ‘faster’ demographic analysis. Besides, since the actual-cohort TFR lacks a calendar time reference point, “the really damaging consequence is that cohort TFRs are always out-of-date” (Brass 1990:456). In plain words, the actual-cohort-based (longitudinal) technique is just too ‘slow’ for contemporary tasks of demographic analysis. Instead, those seeking practical and political outcomes demographers have to necessarily turn to the period (synthetic-cohort-based) demographic analysis — a technique more sophisticated, of more complexity, both theoretically, mathematically, and in its requirements for micro-data processing (and indeed, as I have mentioned above, one that only recently became fullly available), yet the only one that seem to suit the task. Notably, the American (unlike Russian or French) tradition of demographic analysis had always been to consider demographic processes in the context of macro-economic and political development, i.e. in the middle-run (comparable to long waves of economic and technological changes), rather than as secular trends. In fact, Pascal K.Whelpton’s classical works in fertility analysis of the late 1940s -1950s (which had enriched demography with a most important age-and-parity-based model for a synthetic cohort’s lifetime evolution, long before the multi-state life-tables were introduced in the general context), came as but a well-pointed theoretical response on major changes in the US fertility, such as the ‘Baby-boom’, occurred along with the nation’s emergence from the Depression Era into the war and the post-war overall prosperity. In short, whereas the new features of data presently available for demographic analysis made it possible (actually, as never before) to fully implement the period or ‘faster’ demographic analysis, the present demand from the governments and other potential patrons of research demographers necessitate to chose exactly that research path. The path in question, though, is complex, requires researchers to attain some better than before skills in formal demography and calls for support from the areas of mathematical statistics and software development. Hence, to adjust the way in which demographic analysis is taught in Russian universities is, in my opinion, a most important task. The syllabi of supporting academic disciplines, such as statistics and the introductory course of demography, do in my view, also require some alterations. While largely disregarding didactic and pedagogical challenges that the Russian university academia might face, in this paper, I am addressing the said issues from viewpoint of a principal requirement for the academia’s ‘final product’, i.e. a newly graduated Russian research demographer. That principal requirement being to become integrated smoothly into the highly competitive international community of professional demographers. A particularity of Russian academia’s’s history had aggravated the problem, as I see it, by creating an extensive inter-generational gap between the university students in demography who are about to face the above-mentioned integration and competitiveness requirement, and their teachers who had never ever faced it. Indeed, due to certain reasons (which I am going to touch briefly in the very end of this paper, Section 7), the Russian academic and research demographers had been alienated from the mainstream demographic science, functioning instead, for quite a few decades, under a false presumption that demography as a science could possibly remain alive and well (as the late Generalissimo had put it:) “in a single country, considered separately from the others”.
1. Abstract Cohorts: a suggested conceptual framework for demographic analysis. Professor Dmitri I. Valentei (1922-1994), the founder and Head of the Chair for Population Studies and Demography at the Moscow State Lomonosov University, who, until his death, had been indeed the undisputed leader of demography education in Russia, stated repeatedly that demography ought to be viewed as a system of interrelated demographic sciences (or disciplines), each of which possessing its own object and methodology. Following his guideline, one distinguishes the descriptive demography from demographic analysis. The former studies a population as a host of people, an entity described with its composition, or structures, with respect to, say, age, sex, marital status, parity. The evolution of those structures, both in retrospect (population history) and prospect (population projection) is of interest as well. On the whole, descriptive demography borders and supports yet another, applied, discipline, which is commonly termed business demographics. On the other hand, the demographic analysis in its stricter definition is a study of demographic processes considered alienated from the host population. As the matter of fact, that alienation is what chiefly charts a separate field of research for the demographic analysis as a science (1). An immediate rationale behind the alienation is that a population’s evolution is always slow, inertial. Hence, an observed population is largely a product of its own evolution path, which is usually unique, i.e. extremely unlikely to be replicated by any other population. Therefore, considering a regularity of demographic changes in context of the observed population, one gets only a means to derive conclusions with respect to that observed population, not of a more general nature, which was desirable. Instead, the demographic analysis considers a demographic process as a flow of demographic events in context of life of a sole person, an individual, not a population as an entity. It focuses on the quantum of a process under study, which is the lifetime total of the demographic events in question (e.g. the lifetime number of births defines the fertility quantum), and on the tempo, which is the timing of the most important for the study event(s). For instance, the age at death constitutes the mortality tempo, whereas the mortality quantum is obviously a constant, equaling 1.0 In practice, an empirical study has often to be confined to the quantum and tempo indicators only, for more detail indicators are often unreliable due to statistical error of estimation. Being the individual-level counterparts of the macro-demographic indicators, the quantum and tempo quantifications are, of course, of the prime interest for applications. Within the conceptual framework I am herein suggesting the abstract cohort (the adjective abstract is added here to avoid confusion with the common definition) is defined as fully an imaginary body, created strictly for purposes of analysis. Technically: it is to translate the uncertainty associated with demographic events on the individual level into a probability distribution of an artificial population. Or in more common words, an abstract cohort is an imaginary population generalizing (comprising, formally gathering, collecting) individual life paths into an aggregate whose diversity is thus implied. For instance, in an individual woman’s’s life, the first marriage is subject to uncertainty: it might occur in this or that year of her life, or never at all. On the cohort, i.e. an artificial population’s, level that is represented with a distribution by first-marital status (single vs. ever married), tracked by age until the most advanced, upper age limit, when the proportion of currently single equals to the proportion of ultimately never ever married. Formally, an abstract cohort is an imaginary stationary population (i.e. one that allows out-flows, attrition, decrement, but not in-flows, increment), and, for analytic purposes, every abstract cohort is assigned the same initial population size, which is reduced to a unit, i.e. 1.0. The introduction of a cohort as an imaginary population of the initial size 1.0, is a research trick of a precisely the same kind as, say, a convolution of a univariate sample into a distribution function to be studied analytically. The are two ways to link an abstract cohort, i.e. demographic analysis’ ideal object, to the actual, observed, host population. The first one, most straightforward (if most trivial), is provided within the actual-cohort (longitudinal), or ‘slow’, demographic analysis’ methodology. It establishes exact empirical counterparts to the artificial cohorts’ populations, which are just actual birth cohorts in the conventional definition, i.e. contingents of people of the same sex that share a calendar year of birth. Those empirical cohorts had to be observed for the entire length of their lives. Thus the demographic indicators of interest , the quantum and tempo in particular, are obtained with straightforward observation (or a simple tabulation of recorded data), making the estimates always consistent and reasonably reliable, if always much too late. On the other hand, the period demographic analysis’ methodology links the ideal, imaginary abstract cohorts to the empirical, real population as well, but quite in a different manner. It is established by the Synthetic Cohort Principle. The Principle defines a synthetic cohort as an entirely hypothetical, imaginary abstract cohort whose entire life would take place under the conditions observed in the host population within a given calendar period (e.g. under the fertility conditions observed in the host population within the current calendar year). In itself, the Principle does not define a way in which those conditions with respect to a demographic process(es) under study should be specified, hence allowing for different practical ways of measurement. Each of them is based on a theoretical model describing a cohort’s lifetime evolution under the demographic process(es) in question. Nearly always, it is a multi-state (increment-decrement) life table. For instance, for period fertility analysis, one usually applies Whelpton’s age-parity fertility table, which, actually, is a multi-state life table whose states are identified with current parity (see, for instance, an application the Russian fertility in my paper of 1999). A theoretical model chosen to describe the synthetic cohort’s lifetime evolution is then implemented numerically by equating one of its variables which represents an occurrence-exposure ratio to its empirical counterpart (the orientation equation). In Russian, we call the entire procedure an application of the demographic method, while the theoretical model describing a cohort’s lifetime evolution is often referee to simply as a demographic table. While not endorsing a particular way of measurement, the Synthetic Cohort Principle supplies a guideline to judge and compare them. Namely, it commonly can be determined if a certain method represents the demographic process under study more accurately than another does, especially whether the current conditions are reflected more precisely with eliminating the influence of the population’s evolution of the past. An ill-chosen theoretical model of a cohort’s lifetime evolution, or an ill-specified orientation equation might result in inaccurate or even inconsistent estimates for the quantum and tempo. Hence, the period demographic analysis, unlike the ‘slow’ actual-cohort technique, is largely an art of skillful modelling and formal model evaluation, supplemented with (often rather complex) computer micro-data processing. The reward, though, consists in far more practically interesting (if currently not the only interesting) macro-demographic indicators that only the period demographic analysis is in capacity to supply. Of course, the fact that period demographic indicators pertain to an entirely imaginary body of population, the synthetic cohort, in no way implies that they are less 'real’ than those obtained from an actual cohort with a direct observation (2), though such a superstition is still harbored by some Russian (if French) demographers, seemingly due to their ill-fortuned experience with most trivial, conventional (based solely on age-specific rates), period demographic indicators. The transition from the individual life level to the cohort level typically translates individual quantum and tempo values into distributions. For instance, in the case of fertility, the quantum comprises a distribution of the cohort with respect to the lifetime number of children ever born. Such a distribution is convenient to formally represent with parity-progression ratios. If those refer to a synthetic cohort constructed under the Synthetic Cohort Principle, then one usually calls them period parity-progression ratios. Importantly, those indicators are defined uniquely for any cohort, an actual or synthetic alike. What differs is the estimation procedure. In the latter case, it is far more complex and sophisticated than in the former case, where it is reduced to a straightforward tabulation.
2. The theoretical and practical value of solely age-based demographic quantifications and models has been clearly diminishing. And specifically, less importance is attached to conventional age-specific rates. When the supply of data for empirical studies was confined to pre-tabulated quotients, in practice, the only macro-data available for researchers were scores of age-specific rates (e.g., age-specific fertility rates), that is ratios whose denominator represents the size of a population contingent defined solely by its age (a single-year or five-year age interval), drawn from the observed single-sex population , though the numerator could stand for the number of observed demographic events of any kind, defined by the age interval and/or some other dimensions (say, the number of births of a certain order to women of the specified age). As that example suggests, an age-specific rate is not necessarily a proper occurrence-exposure ratio. On the other hand, at present, a demographer (utilizing a professionally written software) can produce a nearly unlimited manifold of the empirical quotients, namely, occurrence-exposure ratios, by deriving them from a collection of micro-data. Because the supply becomes of little limitation, the critical role falls onto the demand side. In theory, as it is presently established, age is recognized as just one of many dimensions a demographic event, or state of a population, can be described with. It is not necessarily a most important dimension, nor is it even an always required for a meaningful description. For instance, speaking about fertility of modern populations of “European culture”, Louis Henry (1954:8) observed: "in practice, the limiting effect of ageing is secondary, and size of family [i.e. parity] becomes the most important factor". In practice of period demographic analysis, the demand for a specific empirical quotient (usually it’s a proper occurrence-exposure ratio), is dictated by a chosen for measurement purposes model of synthetic cohort’s lifetime evolution. However, excepting the well-charted task of constructing a basic (single-decrement) life table for period mortality analysis, under which the conventional age-specific mortality rate is a true occurrence-exposure ratio, the measurement models for period demographic analysis do not seem to generate demand for age-specific rates proper. Because of that, an age-specific rate might only serve for illustration purposes. Yet here too, an indicator obtained as an age-specific variable of the synthetic cohort is obviously more accurate and more consistent than a conventional age-specific rate, which, after all, pertains to an observed population rather than to the synthetic cohort. For instance, it is preferable to illustrate an ‘age profile (or, age schedule) of fertility’ with the age-specific reduced number of births (all birth orders combined), i.e. a variable of the synthetic cohort, which has been implemented numerically with a consistent measurement model, such as Whelpton’s multi-state life table, rather than to rely on the age-specific fertility rate computed conventionally. The respective ‘fertility curves’ plotted against age, however, might appear quite similar on an illustration. Consequently, the role of standardization with respect to age is diminishing as well, though traditionally it is attached a great importance in Russian textbooks and syllabi on demography. One hardly is interested in, say, a crude birth rate (CBR) ‘standardized with respect to age’. Indeed, besides the fact that it is standardized with respect to age only, ignoring the other demographic dimensions (like parity, length of open birth interval), that monstrous indicator, though standardized, remains in its very nature (and in units of measurement) just a crude population-based quotient, not a variable pertaining to the synthetic cohort. The latter, of course, supplies much better measures of the fertility quantum, which, due to the very Synthetic Cohort Principle, are standardized fully, i.e. are completely alienated from the observed population, its structures of any kind. Hence, it is substantial, in my view, to reduce the time (and length in the textbooks) dedicated to standardization by age (and related topics like the Kitagawa decomposition). A good set of exercises (fitted to the student’ self-guided work with a spreadsheet software) would, nevertheless, remain useful. In general, contrary to a tradition of the Russian syllabi in demography, it is wasteful to start the fertility analysis topic (or mortality analysis topic, for that matter) with introduction of the respective crude rate (CBR or CDR), followed by a lengthy criticism of that crude rate. By the same token, whereas the Lexis diagram remains an essential graphic construction to illustrate some simple measurement models of demographic analysis (above all, the basic, single-decrement, life table), and serves as a useful tool for descriptive demography as well, thus earning its firm place in a demography syllabus, a lengthy introduction entitled ‘Time and Age in Demography’ supplemented with definitions of ‘demographic bodies’ of ‘first kind’, ‘second kind’, ‘third kind’, etc. (i.e. rectangles and triangles on the Lexis plane), which the Russian syllabi conventionally favor, I see as waste of time and energy.
3. The actual-cohort-based, or ‘slow’, demographic analysis and the period, or ‘faster’ demographic analysis are not in opposition to each other, but rather they form two different methodologies under the same general approach. In fact, a perceived opposition of those two methodologies is implied solely by the necessity to rely on tabulated age-specific rates, not by the nature of the method. Indeed, when the data were limited to macro-data tabulations, the most common way of measuring a quantum or tempo indicator (i.e. estimating its numeric value) consisted in collecting the supplied age-specific rates either along the Lexis diagram’s diagonals, i.e. life-lines (for the actual-cohort, longitudinal technique) or along its verticals, i.e. time-lines (for the period, cross-sectional technique), and performing computation based on the empirical quotients so collected. That paradigm of collecting, or more accurately, the induction paradigm (for one ascends from available empirical quotients to the indicators of interest with a known, simple way of computation) was prescribed by the nature of data available. With the micro-data sets serving as the main data source, however, the estimation paradigm turns into a deduction one. As soon as it is clear what exactly quantum or tempo indicators are of interest for a given analytic task, one undertakes to measure them either by a simple tabulation (for the actual-cohort, longitudinal technique), or by constructing a formal (measurement) model to describe a cohort’s lifetime evolution and then numerically implementing it with the orientation equations to link the model’s variable to an empirical occurrence-exposure ratio. Finally, the quantum or tempo indicators of interest are produced by that model. Thus, one descends from the indicators of interest down to empirical quotients required for their derivation, selecting an appropriate formal model for measurement. Hence, under the deduction paradigm, the ‘slow’, and the period, ’faster’, demographic analysis methodologies differ in the way of computation (though, to a great extent, indeed), yet they both determine what empirical quotients are needed for the task depending on the task itself, and then derive the needed quotients with micro-data processing, not collecting them from a given supply table. In fact, under the deduction paradigm, the very terms longitudinal and cross-sectional (transversal) became misleading. Hence, I am suggesting terms: period (synthetic-cohort-based) demographic analysis and actual-cohort-based demographic analysis, instead. The major trouble is that under the old induction paradigm, the technique as the way of computation dominated over the demographic meaning of the quantum or tempo indicators to be computed. The really damaging consequence is that, in a student’s mind, a demographic indicator of interest might become too firmly associated with a specific method of its computation, which then serves in lieu of the indicator’s proper definition . For instance, the total fertility rate might be seen as the sum of the age-specific fertility rates, either along the Lexis diagonal (for an actual cohort) or along its verticals (for a synthetic cohort). But of course, that is a methodologically false way of thinking. Correct is to define the total fertility rate as the mean indicator of the fertility quantum, namely the mean lifetime number of children ever born per woman, or the mean lifetime reduced number of children born (for a cohort’s size is set to the unit), with reference to either an actual or a synthetic cohort. There are different ways to compute, or, more correctly to say, different ways to estimate value of the so defined indicator. Particularly, in the case of synthetic cohort, different measurement models and orientation equations might be applied, resulting in different estimates, yet those are estimates for the same very indicator. True, some of the ways of estimation might result in a more accurate, while some ‘s in a less accurate, or even plain biased, inconsistent, estimate. Resting on the Synthetic Cohort Principle, however, the demographer, has certain grounds to judge which way of estimation to prefer. Here is an example. Based on micro-data sets collected by the 1994 Russian micro-census, an estimation of the fertility quantum for the synthetic cohort of 1989 of the ethnic Armenian (Hayck) population of the Russian Federation has resulted in TFR = 2.3462 with the period parity-progression ratio toward a first child, p0 = 1.0710, which is clearly a biased, and even inconsistent estimate. Indeed, the period parity-progression ratio in question represents the lifetime probability for a woman to give birth to at least one child, i.e. not to remain ultimately childless. Obviously, its value can never exceed 1.0. The overestimated p0 raises a suspicion that the total fertility value, TFR, was overestimated as well. The aforementioned bias has occurred because the fertility rising during the 1980s (due largely to the Soviet Union’s effective pro-natalist campaign) had caused the female population composition with respect to parity and open birth interval to diverge significantly from one that would take place were the fertility conditions of the 1980s matching those of the reference year, 1989. However, an ill-chosen estimation method, known as the conventional one, which only takes the age-specific fertility rate into account, ignored the shift in the parity and birth-interval population compositions. A better, i.e. closer corresponding to the Synthetic Cohort Principle, method of estimation, known as the PAD method (a.k.a. the ISFRAD method), which relies on a far more complex model for the synthetic cohort’s lifetime evolution, returned p0=0.9536 (i.e. the childlessness level of about 5 percent) and TFR=2.2217. It is important to realize, though, that a more complex model usually requires a bigger data set for a statistically reliable estimation. In this example, where the sample amounted to just about 10,000 women of reproductive age, the statistical error was substantial. For the TFR, the standard (quadratic) error was estimated as 0.0736.
4. In general, the students should be brought to a clear understanding that numeric values of demographic indicators are always subject to a statistical error (i.e. affected by stocahsticity of the data). The reason for that is neither that estimates are usually derived from a sample (as the opposite to the enire population), nor that demographic events are not always recorded properly by the vital (or civil) registration services. Rather, the key reason lies solely with the fundamental fact that a researcher observes just one and only reality from a host of all possible ‘realities’, which might take place, yet most of them didn’t, though each of them might have a probability to occur nearing that for the reality that actually took place. For instance, whereas a demographic event (death, say) is known to have taken place at a certain calendar year and month, under a certain age of the deceased, and it was recorded correctly and properly, yet, due to innumerable reasons, the death could (equally probably) take place several days before or several days after the day it actually occurred, thus possibly placing the event in question into another calendar month and/or age interval. The same can be said about a marriage, divorce, migration, birth of a child, etc. Generally, empirical data nearly always conjoin with the intrinsic stochasticity. Consequently, measures of demographic indicators are always subject to a certain instability, uncertainty, random variation. That’s why, one talks about estimation of the indicators of interest, rather than their exact measurement, while the uncertainty due to the data’s intrinsic stochasticity is commonly reflected as the (statistical) estimation error. And indeed, presence of the intrinsic stochasticity is what gave birth to mathematical statistics as a science. Of course, the intrinsic stochasticity is present in tabulated (macro-) data as well. But firstly, it is less pronounced, for tabulated data values are normally based on larger original data sets than a typical micro-data collection, and hence the stocahsticity is diminished by averaging to a greater extent. Then secondly, since the data come in a tabulated form, their intrinsic stochasticity is difficult (if ever possible) to detect. In other words, tabulated data do successfully create an illusion of no stochasticity at all. In the case of micro-data, however, the intrinsic stochasticity is almost always possible to detect. Whereas often it is a complicated job, it can not be ignored in a professional study. A most modest task the demographer would seek to accomplish in that regard is to quantify (or to estimate) the magnitude of the estimation error, i.e. to be able to judge to what extent the estimate for an indicator under study is reliable. The conventional measures for that are: the standard (quadratic) error, which is the standard deviation (i.e. the square root of the quadratic variance of the estimate treated as a random variate), and quantiles of the confidence interval. Whereas good academic textbooks in formal demography do offer symbolic expressions (i.e. analytic formulae) for the standard error of estimate referring to selected summary demographic indicators (e.g. Smith 1992:108-117, 242), those (the famous Greenwood’s formula notwithstanding) are limited to relatively simple indicators obtained in the conventional way from the empirical age-specific rates, which is of little interest under the conceptual approach I am suggesting in the present paper, except for applications to actual cohorts. Undoubtedly, to an even greater extent the lack of appropriate symbolic solutions is felt with respect to more complex statistical tasks, such as the statistical inference analysis (i.e. hypotheses testing). Certainly, more advanced and more refineed symbolic quantifications are being developed in the field to serve more complex measurement models, such as Whelpton’s age-parity (multi-state) fertility table describing a synthetic cohort’s lifetime evolution. But of course, since the measurement models themselves are often rather complex, the symbolic expressions for quadratic variances of their summary (quantum and tempo) indicators can not possibly be simple. In fact, their software implementation might require a professional programmer’s job supervised by a demographer well-skilled in the formal methods. Neither is likely to be easily found within the present-day Russian demography academia. Obviously, one has to switch attention from the world of symbolic quantifications to the world of numeric techniques. And indeed, fortunately, there is a new (developed in the late 1980s) statistical technology, which appears so promising that I am not hesitating to suggest is as the principal (if virtually the only) tool to be employed in research studies and in teaching statistical aspects of the demographic analysis. The technology, which belongs to the Monte Carlo (statistical trials) family of methods, can be conceptually reduced to the following. A collection of micro-data (a sample, commonly) that the estimates are based on, which is a formal representation of the observed reality, can be used not only to derive the estimates of interest, but also to generate other collections of micro-data, each of which can be treated as a representation of an alternative ‘reality’ that might have taken place instead of the actually observed one, yet it didn’t. Each of those artificially generated data collections, called a pseudo-sample, appears in quite a similar to the original sample way, and maintains the sample size of the latter. A good software (see my comments below) can generate as many of such pseudo-samples as desired. To each of them, i.e. to each of so represented alternative ‘realities’ the technology attaches the same probability to take place instead of the reality represented by the original data collection (sample) which actually took place and was observed. The estimate of a demographic indicator of interest can be thus derived repeatedly, each time from a new pseudo-sample with an exactly the same estimation routine. In total, an array of pseudo-estimates each derived from its own pseudo-sample becomes so constructed. Since the array can be generated as large as needed, a statistic of interest (such as the standard quadratic deviation) can be computed from it straightforwardly with a reasonable reliability. The technology thus described is referred to as the iterative pseudo-resampling, or, more commonly, as the Bootstrap technique. The latter, slangish, though quite official, name is a reflection upon a certain American saying. For the matter of the Bootstrap’s application to demographic analysis, the following points are substantial:
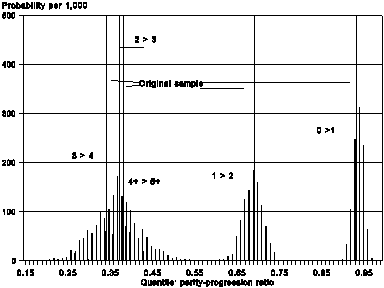
Figures 1 and 2 present an example of the Bootstrap’s application. They refer to a period fertility quantum (period parity-progression ratios) estimates for the synthetic cohort of Estonia’s population, 1989-1993. The sample, which is non-stratified, i.e. self-weighted, contains 5,020 individual records of women’s maternity histories. It was collected within the Estonian FFS project conducted by the Estonian Inter-university Population Research Center, EKDK (Professor Kalev Katus, et al..). The estimates are based on the parity-age, Whelpton’s model (the PA, a.k.a. ISFRA measurement method). Figure 1 shows graphically how stable the estimates are under stochasticity of the data. Along with the estimates derived from the original sample, the Figure depicts those from the Bootstrap pseudo-samples, 1,000 of which were generated. They are represented with a histogram: its X-axis positions the estimates, while the Y-axis assigns Bootstrap frequencies (empirical probabilities) to them. Visibly, the estimate for the lifetime probability to give birth to at least on child, p0, and therefore, the childlessness level, 1-p0, are fairly stable: their dispersion along the X-axis is pretty small. The reliability, however, declines fast with parity. That is reasonable, for the effective sample size shrinks with parity considerably. Interestingly that, judging from the Figure, it is not possible to distinguish statistically the estimates for parity-progression ratios above parity one:, p2, p3, p4+, whereas their estimates derived from the original sample appear distinct. In other words, the differences in the estimates for positive parities are statistically insignificant, i.e. due to stochasticity of the data.
Figure 2 presents yet another perspective. Each line on the graph corresponds to its own Bootstrap pseudo-sample (100 of those, in total). One is interested in statistical stability of an empirical regularity that appears from the original sample. Namely, one observes an inequality p4+= 0.380 > p2 = 0.369, i.e. the lifetime probability to give birth to a fifth or a higher-order child appears to exceed that for a third child (graphically, the ‘tail’ of the parity-progression curve is up). Such an inequality (which I observed for several populations of Easter Europe, and Russia) can be interpreted as a presence of a small contingent with a distinctively higher fertility level. Since it is small, its influence on the overall fertility level, measured with TFR, is not very well detected, yet an usually high probability to advance to upper parities, p4+, indicates its impact. However, could it be that the inequality in question is just a statistical artefact, i.e. a consequence of the data stochastisity? Figure 2 speaks in favor of that conclusion. In the example studied, the Bootstrap estimate for the probability of the inequality in question amounts to only 0.72. The Bootstrap can be applied to two-sample problems of statistical inference, as well. For instance, one could test statistically a hypothesis that the total fertility rate (or the childlessness level) of the ethnic Estonian population exceeds that for the ethnic Russian population of Estonia. The respective algorithms are given, e.g., in the above-mentioned textbook of B. Efron and R. Tibshirani (1993:221).
5. Teaching the elementary probability theory and statistics to demographers. Since turning to micro-data allows to attach more attention to statistical aspects of demographic analysis in general, it becomes highly important to ensure relevance of the background training courses in the probability theory and statistics, which are normally presented to students in demography prior to their taking systematic courses in demography itself.. Years of my experience in reviewing manuscripts in formal demographic fertility analysis submitted for publication in major journals, as well as my personal communication with scores of demographers, students included, both in the United States and abroad (in Germany, Estonia, and particularly in Russia) had lead me to a sad conclusion that certain greatly important areas of the modern probability theory and statistics are learned to an unsatisfactory degree, preventing the demographers from their fluent applications to research problems in demographic analysis. That finding came as a surprise to me, because the areas in question are not ones of higher mathematical complexity. On the contrary, they seem to be of greater formal transparency, more intuitive, and, importantly, more probabilistic in nature than the other, more classical areas of the probability theory and statistics, which the host of demographers (excepting, possibly, older generations of the Russian ones) had seemingly mastered fairly well. My feeling is that a kind of psychological barrier (undoubtedly, due to education the demographers had been exposed) has been shielding the areas in question from the common sense of a research demographer. Nobody appreciates such a psychological barrier to be repeatedly re-built in the minds of each new cohort of the Russian demography students. Consequently, as I see it, strengthen either of the two topics described below would fall with the general task of making the training in the probability theory and statistics more relevant to requirements of teaching demography, but it also is designed to contribute to a more general strategy. Namely: to make the Statistics syllabus less formal, lighter mathematically (possibly, at the expense of greater computational complexity), more intuitive, encouraging students’ probabilistic way of thinking, their intuitive feeling of the intrinsic stochasticity, statistical stability/reliability of the demographic estimates, while not requiring a substantial enrichment in the supporting courses of basic calculus and linear algebra.
6. For teaching purposes, one has to clearly separate statistics from econometrics, as well as to separate econometrics from demography. As I argued before (Section 5), the main task of an academic course in Statistics for demographers is to encourage students’ probabilistic way of thinking, their intuitive feeling of the stochasticity, statistical stability/reliability of estimates, rather than to arm them with a host of formal tools. That is because, the well developed statistics’ tools are not likely to be applied directly for practical problems in modern demographic analysis (for they are more complex than the classical tools can presently handle). The Bootstrap, as generally the Monte-Carlo family of numerical techniques, serve well to the purpose of encouraging the probabilistic intuition. On the other hand, certain mathematical tools, though they have been traditionally taught within the Statistics’ syllabus, are, in my view, rather discouraging with respect to a probabilistic way of thinking. The multi variate linear regression appears to be a tool of that kind. The practice of its application (beyond artificial examples offered in textbooks on Statistics) is, virtually never in agreement with the probabilistic background of the method. Indeed, the assumptions on probability distributions that underline statistical inference with respect to the regression estimates, such as the normality and homoscedasticity (holding the variance constant) of the residuals, are seldom checked (in part, because that is not an easy task), and, actually, are seldom met. What’s more, not surprisingly, the statistical inference itself (i.e. hypotheses testing) is seldom invoked at all. Instead, for most practical purposes, the regression is considered a deterministic, not a probabilistic, approximation. The same I can say about another powerful and useful tool, the principal component technique (PCA). Either of those two tools, however, is proven to be quite instrumental for application in formal demography, especially in technical tasks. In this regard, it would be reasonable, in my judgement, to transfer both those topics from the course of statistics to either the course of matrix algebra (where they can be presented as purely deterministic tools for approximation), or to the course of econometrics proper, where again, they can be taught in deterministic context. Thus ‘lightened’, the Statistics syllabus would gain some better methodological purity, for sure benefits of the students in demography. Where the divide is seen even more of didactic importance, is the separation of demographic studies in general from the econometrics’ methodologies. Indeed, demography and econometrics are different in the core. Demography, in its very nature, is a balance science. It views the movement of population as flows of physical substance of a kind (say, a liquid), which obeys the balance laws, i.e. maintains the total volume unchanged. That view holds equally true for either an actual population (e.g. in the cohort-component technique), or an imaginary population of a synthetic cohort flowing lifetime-long through a multi-state life table, much in a way water flows through a network of pipes. Demography, therefore, appears an exceptionally lucky, ‘clear’, science (en par with, say, classical mechanics) that does not need to ‘fish’ empirical regularities from dark waters. On the contrary, the ‘fishing’ for either deterministic or stochastic empirical regularities is seen as the prime task for econometrics, with (non-linear) regression serving as its prime tool. The production functions of, say, Cobb-Douglas or CES type is a typical example of econometrics’ ‘Black Box’ model, fished out from the (sparse) empirical data. A pointed (if sharply satirical) critique of a popular regression model applied to a demographic process is given by Máire Ní Bhrolcháin (1997:362) It is important, in my opinion, to discourage students in demography from ‘Black-Box’ type econometric models (though psychologically attractive they are), with offering better-selected research problems from the field of demography per se, while censuring questionable ‘demo-economics’ formal constructions from the curricula.
7. What was the key cause of the Russian demographers’ alienation? Lastly, I am returning to an issue I raised in the very beginning of this paper: the very regretful fact that research demographers of Russia (as well as the Russian academia) happened to function, for decades, under a false presumption that demography as a science could possibly remain alive and well “in a single country, considered separately from the others”, i.e. alienated from the mainstream demographic science. The darkest period of that alienation fell, in my opinion, on the late 1940-s until the late 1960s. Back then, even the most distinguished, classical, works in demographic theoretical methodology (at the first place, publications of Pascal K. Whelpton, and Louis Henry) were left unnoticed by the Russian demographers, with a very rare, though notable, exception of Leonid E. Darsky (1930-2001). Rather, during those dark decades, the main body of Russian demographers was exemplified by, while actually preponderated by, Boris Caesar Ulanis (1906-1981), whom many followed. A demographer, in my judgement, of rather modest scientific achievements and abilities, he, after his early works on population history had been published in the 1940s, turned instead to writing semi-popular pieces, often placed in general-purpose periodicals, thus seeking (and indeed finding) recognition from the non-professional populace. In my view, as of now, the time has come to understand clearly what had caused that unfortunate alienation, for which not just those involved, but younger generations of Russian students in demography have now to pay dearly. One observes that the alienation in question had not started in an immediate aftermath to the October (1917) Socialist Revolution. In fact, the 1920s works of the Russian demographers fell well in the then-mainstream of the world demographic science. A good (and not the only) example is Michael W. Ptookha’s works on mortality in the Ukraine. The alienation occurred later, in the 1930s. True, those were the years when the Soviet Government was hastily erecting the infamous ‘Iron Curtain’ around the nation. Although admittedly hard, the ideological pressure imposed since then was not so overwhelmingly heavy as the urban legends of today tend to portray it. In my own recollection, during the 1960s (when the ideological censorship was hardly any lighter than in the 1940s), anyone (even myself, then a secondary-school schoolboy) could freely access a Western scientific journal or a research book from a major library (The State Lenin Library was my own choice). However surprisingly, the major, leading world demographic journals and research books were left unread by the Russian professional demographers. A Russian-language book entitled Mathematical Techniques in Demography supplies an instructive example. Its author, Elijah G. Wenezkey (1914-1981), a Professor of repute, had been teaching both statistics and demography to scores of students in a highly-regarded Moscow university college. The book, which was supposed to serve as a textbook, offers a survey of mathematical models and methods in population studies (with emphasis on basic life tables). Respectively, it contains references to a quite a few publications in foreign languages, including some rare original ones that had been released in the 19th century and the early 1900s. The most ‘recent’ foreign-language source cited, though, was a certain article published in 1931 in German. Noticeably, instead of direct references to the UN Manuals on demographic techniques, published in the 1950s and 1960s in English, those were done to their Russian translations. The book itself went in print in 1971, which is precisely 40 years after the ‘recent’ of its most foreign-language citations. That surely begs for explanation! As I see it, the key reason here is one of a common-life, rather than of political, nature. Namely, it consists in lack of fluency in the English language. The older generations of Russian demographers who, in the beginning of the century, had graduated from Russian Imperial universities and/or universities of Europe, were, of course, well fluent in the German and French languages ‘s the main (if not the only) languages in which scientific research works (demographic studies included) were then published. That lasted throughout the 1920s. Yet, since the 1930s, the English language had been rapidly substituting the German and French as the major international language of science and technology. While the reasons for that were chiefly political, the substitution trend was quite definite and sustained, paralleling the migration drain of major researchers (while sometimes, entire scientific units), as well as intellectuals ‘at-large’ from Europe to North America. In 1932, notably to the demographers, a most renowned German-language paper of Robert Rene Kuczunski, the one where he had introduced the Total Fertility Rate (TFR) as a summary measure for the period fertility quantum, originally presented at the XIV International Congress of Hygiene and Demography (Berlin,1907), was translated into English and re-published. The domination of the English language became even more pronounced after the War, along with the position of the United States in virtually all spheres of international communication getting stronger at the expense of those of the older European nations. To assess the situation in demographic studies as of the very end of the 20th century, I have tabulated the full list of citations that appeared in the Population Index 1999, No. 4 (which was, unfortunately, the last issue of the Population Index published), about 1,500 totally, by the language of their original publication. Thus, from the entre world of publications in population studies, 77.8 were published in English, 9.7 percent in French, 3.9 percent in German, while the remaining 8.6 percent embraced all the other languages (Present were citations in: Spanish, Italian, Dutch, Japanese, Persian, Russian, Serbian, and Thai languages.) Importantly, works on methodological issues and formal demography appeared exclusively in English and French, while the local-language publications were mainly those on empirical case studies. The leading international journals in population studies (which often are the only ones read regularly by the host of professional demographers) are in English and French only, save the only exception of a major German-language journal (other demographic journals published in Germany and Austria are in English.) As of 2001, the oldest and the most renowned of leading demographic journals, Genus, published in Rome (Italy), which used to print papers in English, French, or Italian, had changed to an English-only publication. The said ascertains beyond any reasonable doubt that fluency in the English language became (perhaps, as early as by the mid-1930s) an absolute necessity for staying professionally connected to the mainstream demographic research and science. Unfortunately, by the mid-1930s, the older generations of Russian demographers, those who had received their education during the good old Imperial time, (if survived) became too old (if too frail) to master a new language. On the other hand, the younger generations, whose graduation fell in the Soviet epoch, had, seemingly, presumed that the protecting ‘Iron Curtain’ would stay forever, and thus there was no need to learn any foreign language at all, while enjoying the privileged conditions that ‘the single country, considered separately from the others’ had been holding for them. But of course, the current generations of Russian university students in demography can not possibly afford to rely on that presumption.
Endnotes (1) One views that alienation as a purification of the research field. To express its intrinsic meaning, I am taking liberty to invoke the literature, hence borrowing much better words than my own. Thus, in the words of Rudyard Kipling: ‘If I have taken the common clay ‘If thou hast taken the common clay, References Barkalov, Nicholas B.; and Jürgen Dorbritz. (1996). "Measuring period parity-progression ratios with competing techniques. An application to East Germany", Zeitscherift für Bevölkerungswissenschaft 21(4): 459-505. Barkalov, Nicholas B. (1999). "The fertility decline in Russia, 1989-1996: a view with period parity-progression ratios", Genus 55(3-4): 11-60. Brass, William. (1990). "Cohort and time period measures of quantum fertility: concepts and methodology". In: H. A. Becker (ed.) Life histories and generations. Vol. II: 455-476. The Netherlands Institute of Advance Studies in the Humanities and Social Sciences. Utrecht, the Netherlands. Efron, Bradley; and Tibshirani, Robert J. (1993). An Introduction to the Bootstrap. Chapman and Hall: NY. Henry, Louis. (1954). "Fertility according to size of family: application to Australia", Population Bulletin of the United Nations 4: 8-20. Ní Bhrolcháin, Máire (1992). Period paramount? A critique of the cohort approach to fertility. Population and Development Review. 18(4):599-630. Ní Bhrolcháin, Máire (1997). "Future prospects for population research in the United Kingdom". In: J.-C. Chasterland L. Rousell (ed.) Les contours de la démographie: au seuil XXIe siècle. INED: Paris [France]: 337-368. Rallu, Jean-Louis et Laurent Toulemon. (1993). "Les mesures de la fécondité transversale. I. Construction des différents indices", Population 48(1): 7-26. "Les mesures de la fécondité transversale. II. Application à la France de 1946 à 1989", Population 48(2): 369-404. [Abridged English translation. (1994). "Period fertility measures. The construction of different indices and their application to France, 1946-89", Population: An English Selection 6: 59-94.] Smith, David P. (1992). Formal demography. Plenum: N.Y. and London.
|